提锥规划的原因是因为这个技巧可以用求解一些鲁棒优化导致的问题, 比如我们在之前使用范数2来选择不确定集合 的时候, 其最终形式就涉及锥规划问题了.
首先回忆标准形式的LP:
s.t.
我们可以拓展该LP模型来包含非线性. 前两行可以讨论的不多, 但是最后一行的非负条件我们可以进行改动. 这里我们在比较两个向量 和
的大小, 我们可以写成
. 这并不是唯一的定义方法, 这是我们引入非线性的突破点.
从代数角度
" " 定义了一个"good"排序, 因为其满足如下性质:
Partial order (偏序关系):
1) 自反性 (Reflexivity):
2) 反对称性 (Anti-symmetry): and
3) 迁移性 (Transitivity): and
同时, 还有:
4) 齐性 (homogeneity): and
5) 可加性 (additivity): and
这允许我们证明:
- Farkas lemma: certifying (in)feasibility of linear system
- Strong duality: certifying optimality of a pair of primal-dual LPs
从几何角度
考虑集合
该集合是闭集, 且 , 且
的内部(也就是不要边界)
(严格正).
此外, 其还是个 尖锥 (pointed cone), 其需要满足:
1) :
2)

3)
这给了我们对 的直观理解:

现在我们就有了如下问题: 代数角度中, 是否 "" 是唯一满足(1)-(5)的关系? 几何角度中, 是否
是唯一包含原点和非空内部的closed pointed cone? 答案是否定的, 这里我们可以举两个标准的例子:
- 二阶锥 Second-order/Lorentz cone
其中
为标量,
为向量.
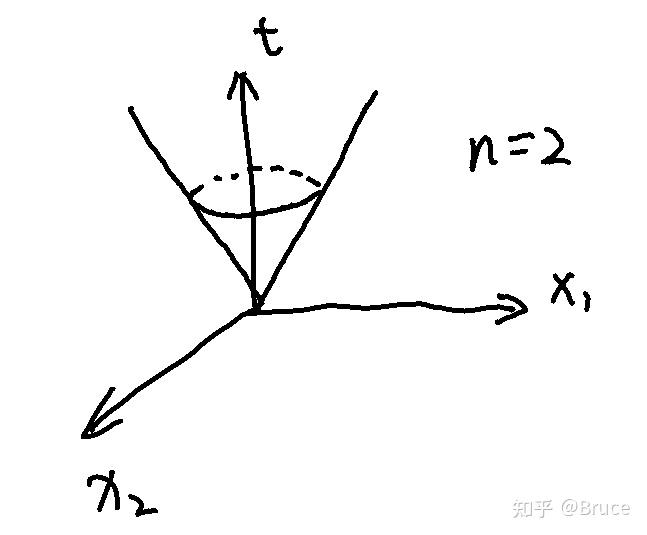
练习: 证明 with
且
是closed pointed cone. 确定
.
练习: 证明 不是一个多面体 Polyhedron - finite intersection of halfspaces.
我们也可以从代数角度去考虑: 我们重新定义order " " 为:
练习: 证明order" "是good order.
2. , 其中
为
的对称阵, 且满足半正定的性质. 这个集合被称为 半正定锥 (semidefinite cone). 比如当
时,
可以选择的元素有3个, 可以写为
, 则其必须满足以下条件:
若 , 我们可以选择的元素就有6个, 则更加复杂.
练习: 证明 是一个closed pointed cone, 其中
且
. 确定
.
PS: 这里不难发现 与
不一样, 因为
是三维的,
是6维的, 并不是每个维数都有, 而
每个维数都有.
我们考虑order" "的定义为
.
练习: 证明order" "是good order.
有了上述两个方式, 我们就可以去重新定义LP了:
现在我们假设有一个closed pointed cone , 其包含 0 与非空内部, 我们可以构建conic LP:
(P)
这里 是在欧几里得空间的内积, 如果
和
都是向量, 那么我们可以等价写成
; 同样地, 这里我们可以写成
. 唯一的不同是这里
不再
, 从而体现了非线性的约束条件.
它有一个对偶问题:
(D)
PS: 这里 和
指的是 infimum and supremum, 也就是一个集合最大的下界/最小的上界
其中 是
的对偶锥.
怎么理解呢? 如果我们要求内积为非负, 那从几何角度来说, 就要求夹角<90°, 我们可以从下图来理解:
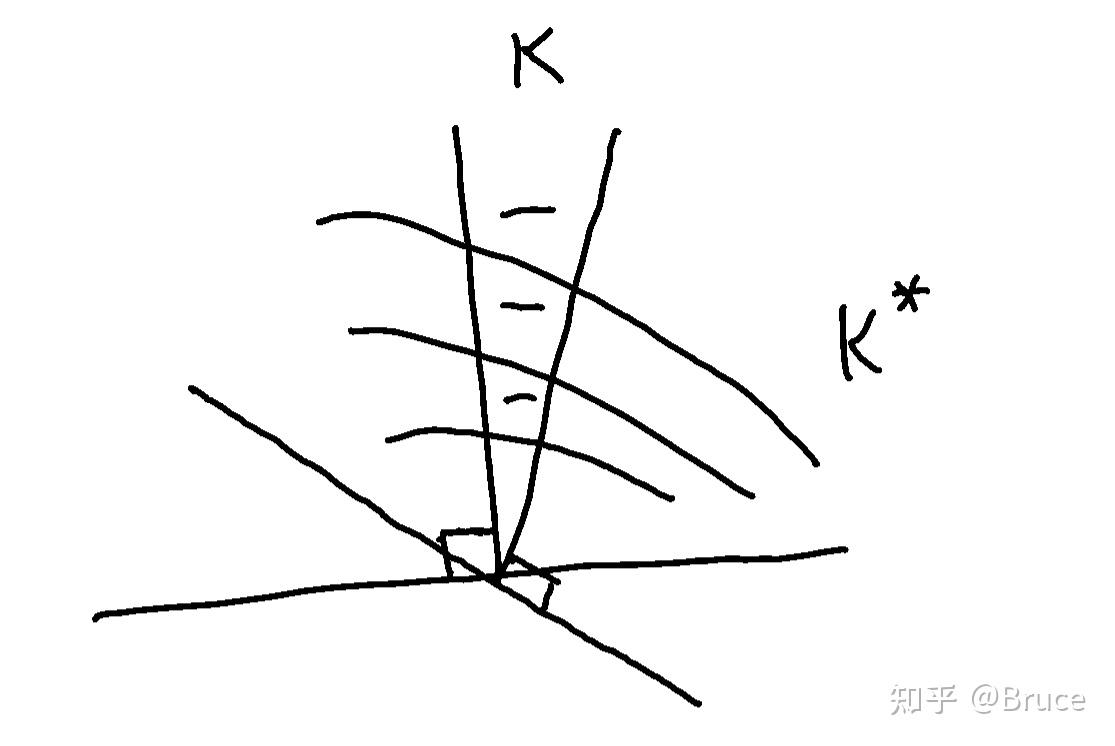
就是找到距离 两条边界的90°的另外两条边, 其构成的锥就是
.
那么我们可以怎么描述这两个问题呢?
(P) 中有线性目标函数, 等式的约束条件, 决策变量必须要在锥中;
(D) 还是在优化一个线性目标函数, 但对于约束条件, 我们先看左边的项 , 它是对决策变量
的一个仿射 (affine) 函数, 因此我们可以将(D)描述成, 我们在优化一个线性函数, s.t. conic constraint on affine map of
.
Proposition: 若 是一个closed pointed cone, 其内部非空, 且
也满足, 则 (P) 和 (D) 性质相同.
练习: show that are self-dual, i.e.,
我们可以从几何的角度入手, 比如对于 :
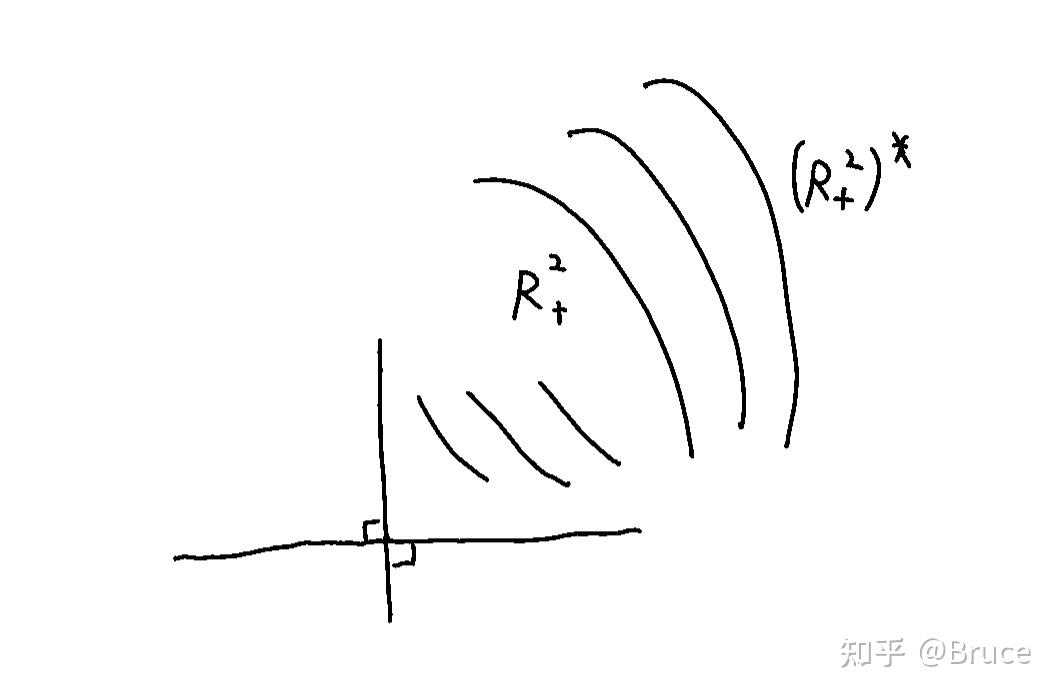
接下来我们介绍一些例子:
(1) SOCP 二阶锥规划
(P)
s.t.
(D)
s.t. 因为
在文献中, 通常写成如下形式:
令 是一个列向量
那么, 可以写为:
(回忆
中,
)
其中 是一维的,
是n维的,
也有其他的方法去写 :
(2) SDP 半正定规划
(P) 要求
, 对两矩阵内积
s.t.
可知
是一个矩阵
(D)
s.t.
, 这两个矩阵都是对称的, 最后的差仍为对称阵
接下来我们举个例子, 回忆:
(RLC)
当 , 我们有:
(RLC)
因为左右项都是对 的仿射函数, 可以看出这是个二阶锥 (SOC) 约束. 也就是, 虽然我们的RLC是线性的, 但如果我们使用2范数来选择不确定集, 那么我们就会得到一个SOC约束条件.
那为什么我们要大费周章讨论LP, SOCP和SDP呢? 就是因为它们是非常标准的凸问题, 有许多成熟的工具和solver, 而且这三类问题可以在多项式时间内求解.


