中值定理的一个问题及其推广

  盛煌资讯     |      2024-01-23 04:55
（川大2015）设 f 在 [0,1] 上可导， f(0)=0,f(1)=1 ，证明：存在 a,b\\in(0,1) 使得 \\frac{1}{f'(a)}+\\frac{1}{f'(b)}=2\\\\

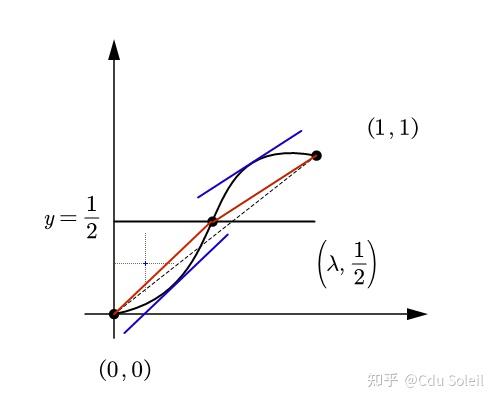
分析:初次看这题的时候，想过许多方法，但都不太好控制(还考虑过辅助函数 g=f-x )，它的几何意义还是很明显的,但证明的话是有些取巧的。

证明：设 f 在 [0,1] 上可导，因此 f 在 [0,1] 上连续，根据介值定理，知道 f(\\lambda)=\\frac{1}{2},(0<\\lambda<1) ,

根据中值定理就有 \\frac{1}{2}=f(\\lambda)-f(0)=f'(a)(\\lambda-0),\\\\ \\frac{1}{2}=f(1)-f(\\lambda)=f'(b)(1-\\lambda).\\\\ 从而我们易见有 \\frac{1}{f'(a)}+\\frac{1}{f'(b)}=2,a,b\\in(0,1). .

笔者注意到这是裴礼文的一道经典题，于是有如下推广

（推广）设 f 在 [0,1] 上可导， f(0)=0,f(1)=1 ， k_1,...,k_n 为 n 个正数.证明：存在一组互不相等的 x_1,x_2,...,x_n\\in(0,1) 使得 \\sum_{i=1}^n{\\frac{k_i}{f'(x_i)}}=\\sum_{i=1}^n{k_i}\\\\

分析:我们仿造前面特殊情况，很容易得出证明方法

证明:令 \\displaystyle m=\\sum_{i=1}^n{k_i} ,首先对要证的式子进行归一化， \\sum_{i=1}^n{\\frac{\\lambda _i}{f\\prime(x_i)}}=1,\\lambda _i=\\frac{k_i}{m}.\\\\ 我们选取点 0=c_0<c_1<c_2,...<c_n=1 ,使得 f(c_i)=\\sum_{l=1}^i{\\lambda _l},i=1,...,n\\\\ 这是成立的，因为f 在 [0,1] 上连续，且 \\displaystyle0\\le\\sum_{l=1}^i{\\lambda _l}\\le1 ，根据中值定理有 \\lambda _i=f(c_i)-f(c_{i-1})=f'(x_i)(c_i-c_{i-1}),i=1,....,n\\\\ 所以就有 \\sum_{i=1}^n{\\frac{\\lambda _i}{f’(x_i)}}=\\sum_{i=1}^n{c_i-c_{i-1}}=c_n-c_0=1\\\\

命题易见 \\sum_{i=1}^n{\\frac{k_i}{f'(x_i)}}=\\sum_{i=1}^n{k_i}\\\\ 成立

经典！